Unzipping Immutability

This page contains the materials for my talk “Unzipping Immutability”. Here are some past presentations:

You can use this page in two ways:

as a reference/refresher on the concepts covered in the talk;
as an interactive playground where you can try the same commands I presented.

Here is an overview:

Immutable data structures
Lenses
Zippers
Useful resources

Throughout this page we will assume the following declarations (each section might add its own):

import reftree.core._
import reftree.diagram._
import reftree.render._
import reftree.demo.Data._
import scala.collection.immutable._
import java.nio.file.Paths
import Diagram.{sourceCodeCaption ⇒ diagram}

To start an interactive session, just run

$ sbt demo
@ render(List(1, 2, 3))

and open diagram.png in your favorite image viewer (hopefully one that reloads images automatically on file change). You will also need to have GraphViz installed. The interactive session already has all the necessary imports in scope.

Immutable data structures

// extra declarations for this section
val renderer = Renderer(
  renderingOptions = RenderingOptions(density = 100),
  directory = Paths.get(ImagePath, "immutability", "data")
)
import renderer._

Lists

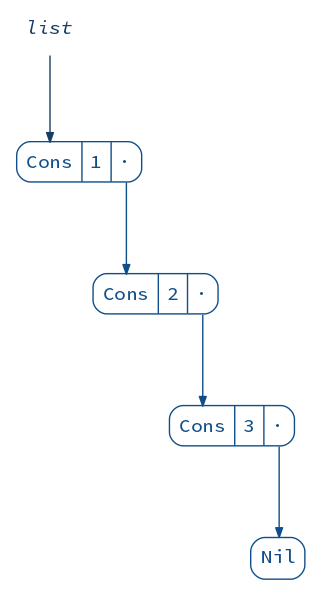
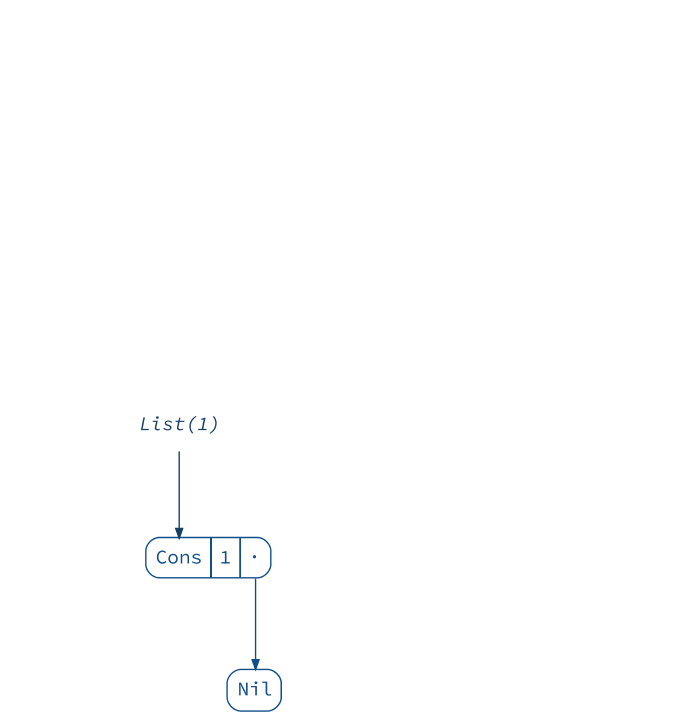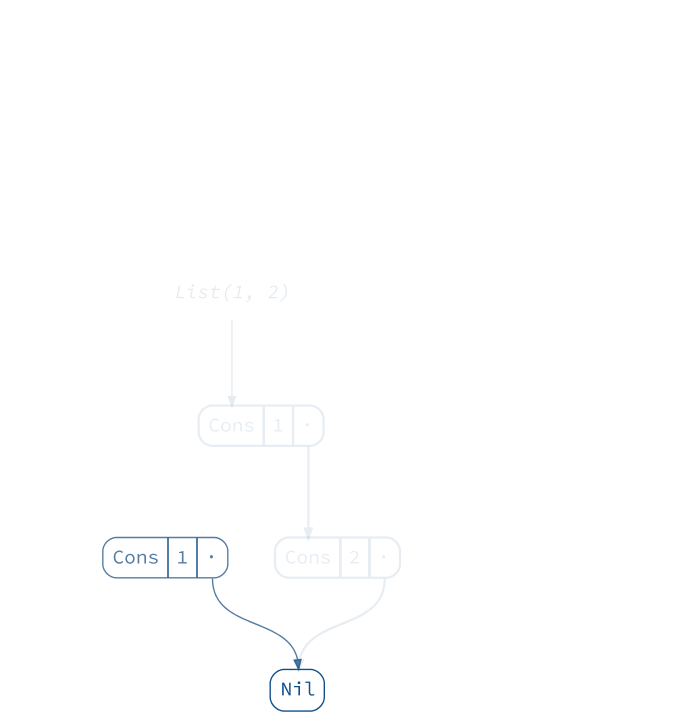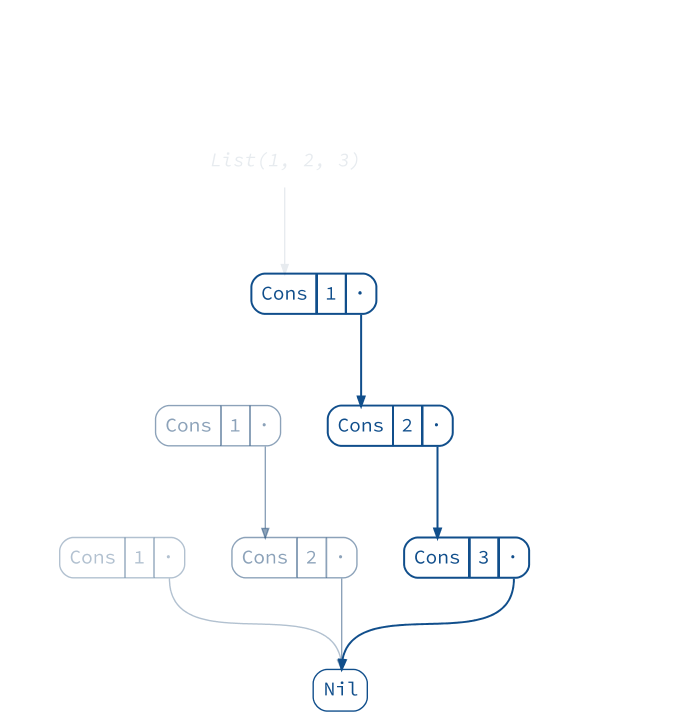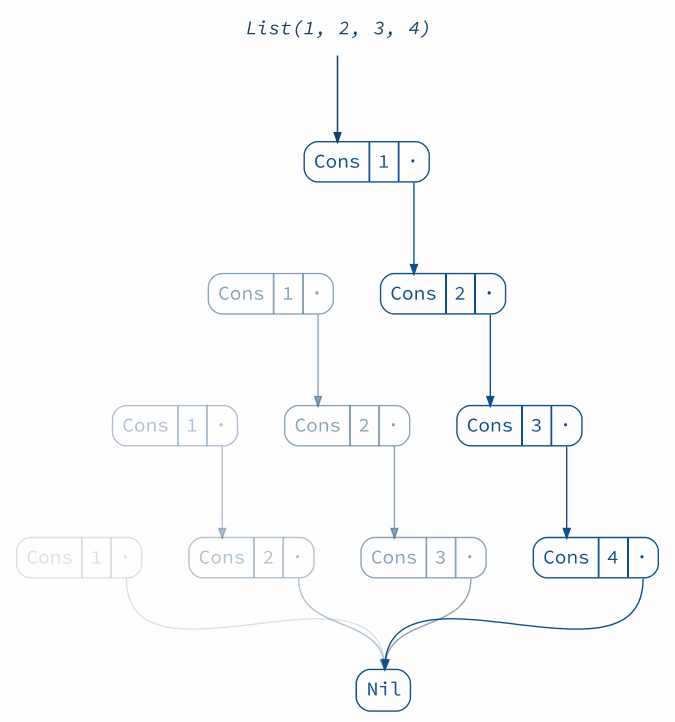
We’ll start with one of the simplest structures: a list. It consists of a number of cells pointing to each other:

scala> val list = List(1, 2, 3)
list: List[Int] = List(1, 2, 3)

diagram(list).render("list")

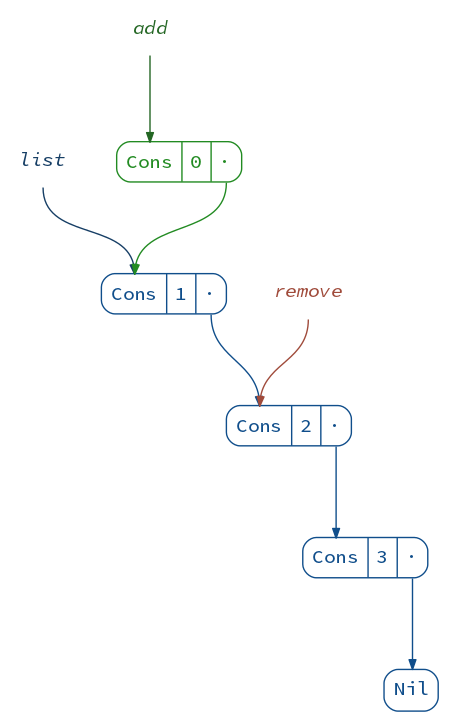
Elements can be added to or removed from the front of the list with no effort, because we can share the same cells across several lists. This would not be possible with a mutable list, since modifying the shared part would modify every data structure making use of it.

scala> val add = 0 :: list
add: List[Int] = List(0, 1, 2, 3)

scala> val remove = list.tail
remove: List[Int] = List(2, 3)

(diagram(list) + diagram(add) + diagram(remove)).render("lists")

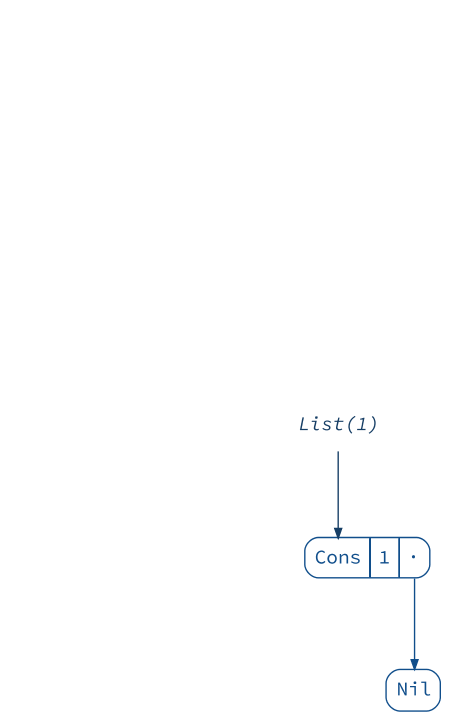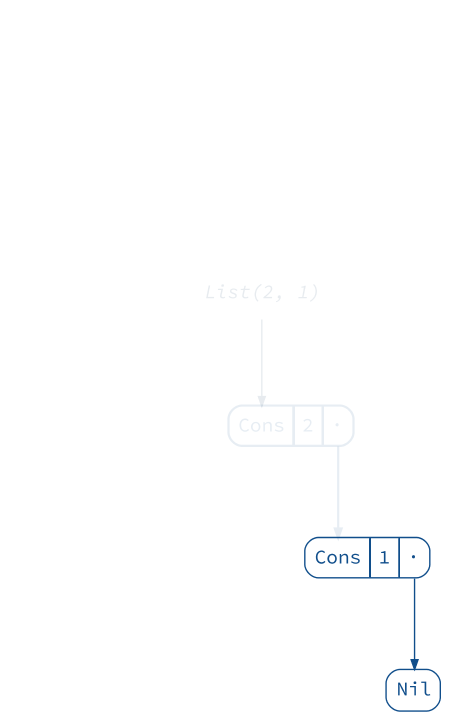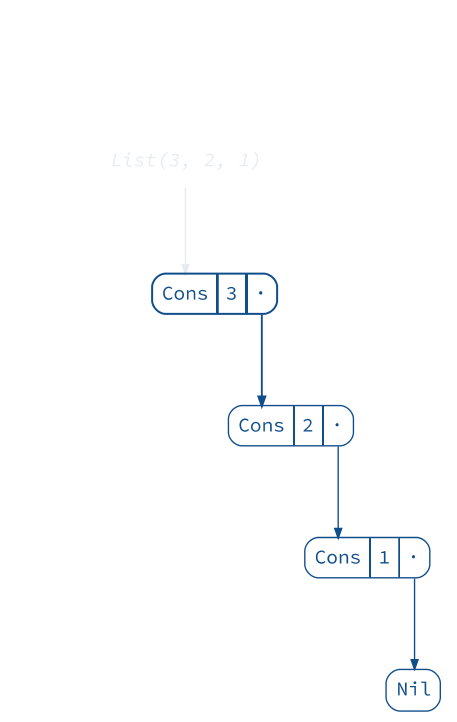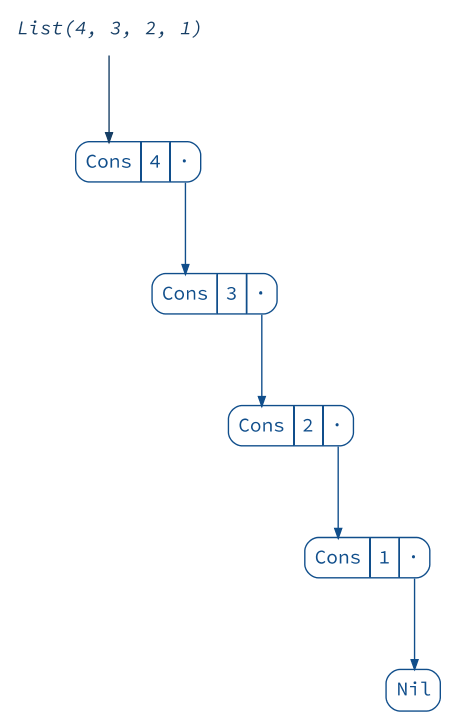
However we can’t easily add elements at the end of the list, since the last cell is pointing to the empty list (Nil) and is immutable, i.e. cannot be changed. Thus we are forced to create a new list every time:

(Animation
  .startWith(List(1))
  .iterate(_ :+ 2, _ :+ 3, _ :+ 4)
  .build()
  .render("list-append", tweakAnimation = _.withOnionSkinLayers(3)))

This certainly does not look efficient compared to adding elements at the front:

(Animation
  .startWith(List(1))
  .iterate(2 :: _, 3 :: _, 4 :: _)
  .build()
  .render("list-prepend"))

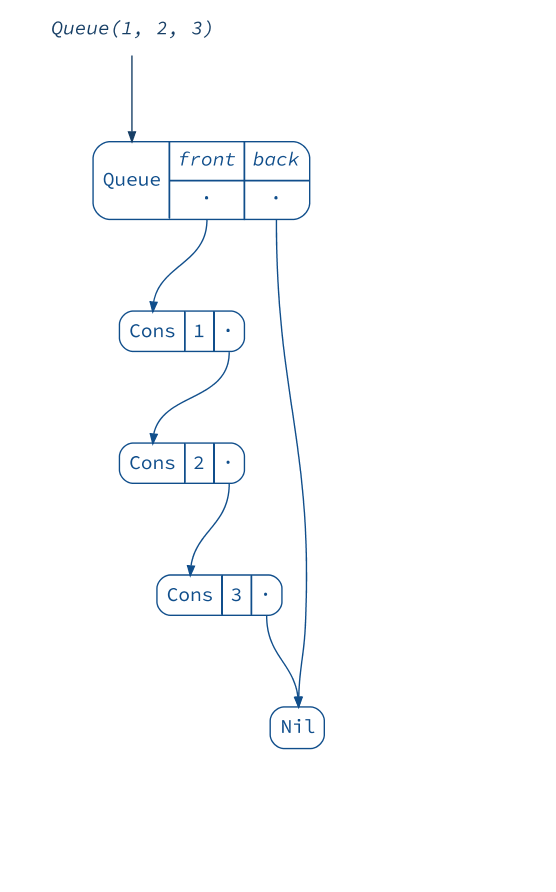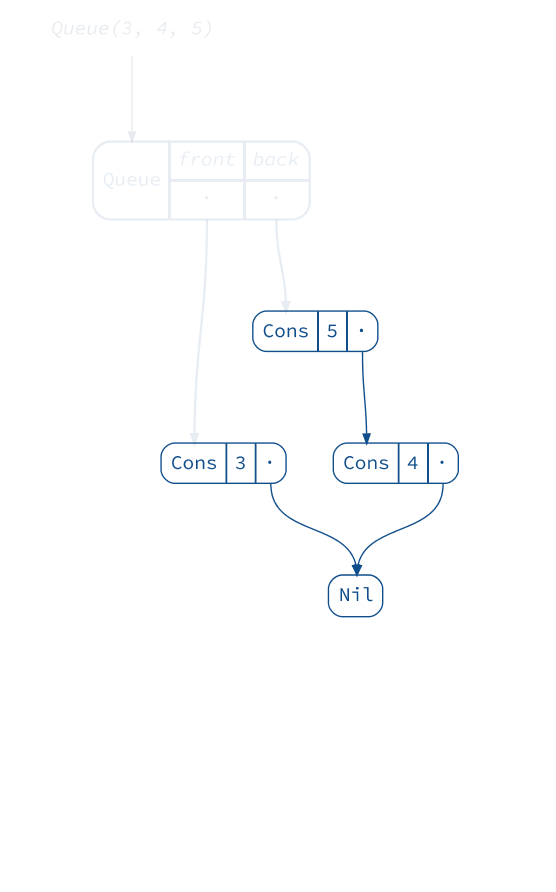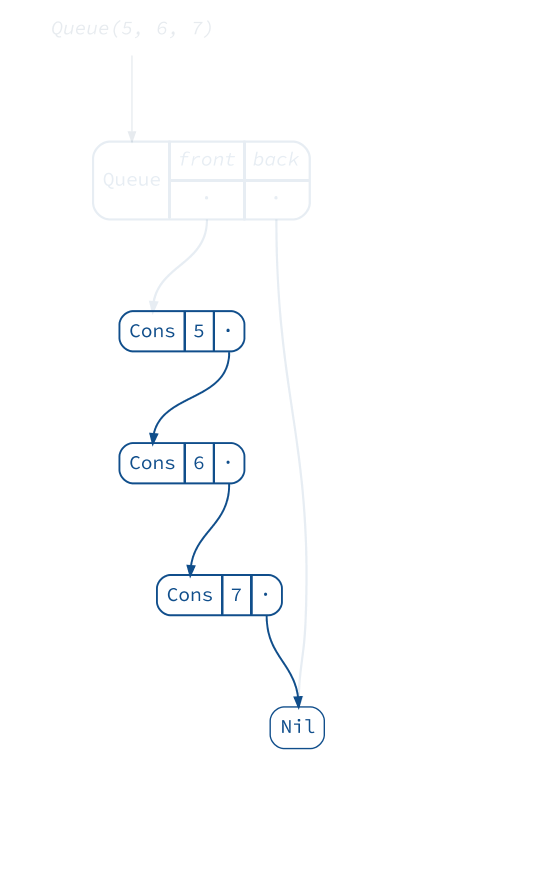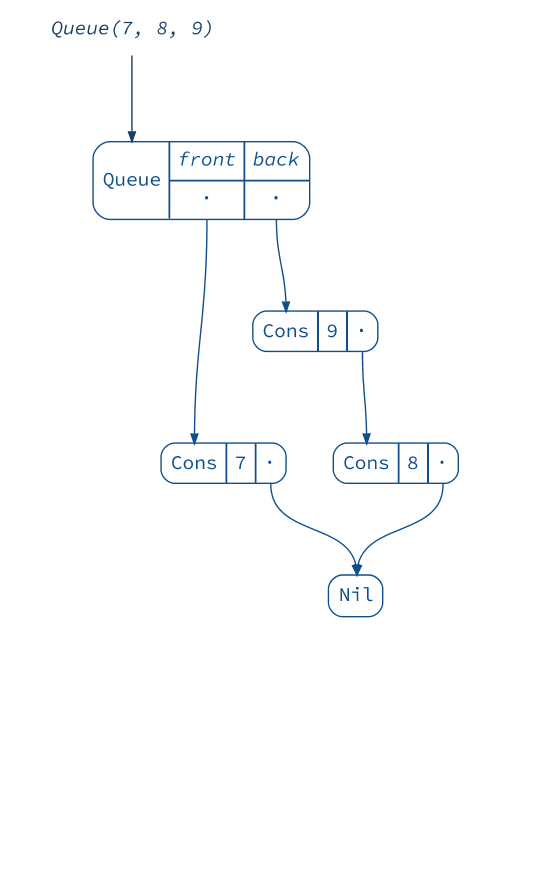
Queues

If we want to add elements on both sides efficiently, we need a different data structure: a queue. The queue below, also known as a “Banker’s Queue”, has two lists: one for prepending and one for appending.

scala> val queue1 = Queue(1, 2, 3)
queue1: scala.collection.immutable.Queue[Int] = Queue(1, 2, 3)

scala> val queue2 = (queue1 :+ 4).tail
queue2: scala.collection.immutable.Queue[Int] = Queue(2, 3, 4)

(diagram(queue1) + diagram(queue2)).render("queues", _.withVerticalSpacing(1.2))

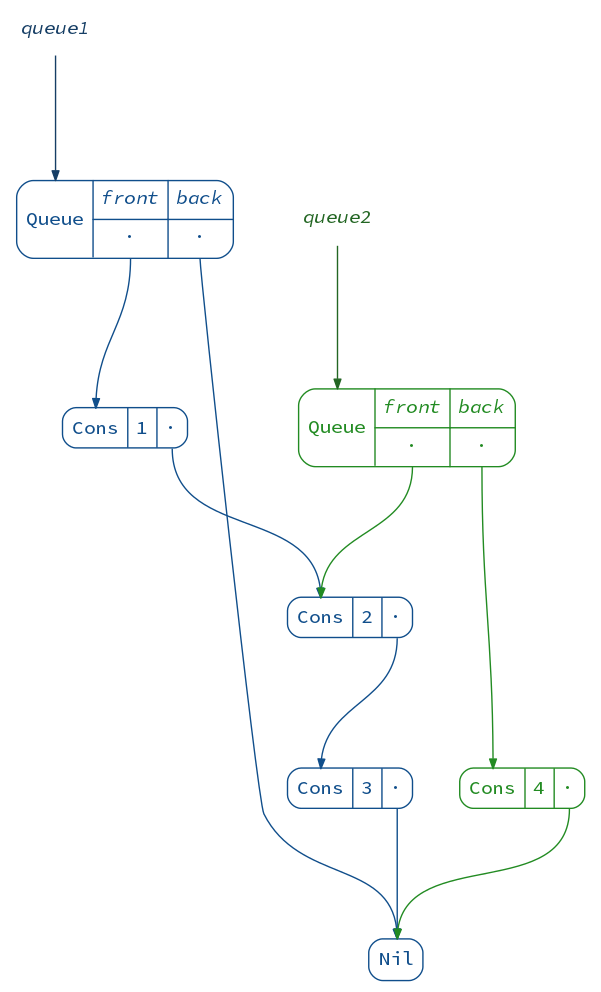
This way we can add and remove elements very easily at both ends. Except when we try to remove an element and the respective list is empty! In this case the queue will rotate the other list to make use of its elements. Although this operation is expensive, the usage pattern intended for a queue makes it rare enough to yield great average (“ammortized”) performance:

(Animation
  .startWith(Queue(1, 2, 3))
  .repeat(3)(_.iterate(2)(q ⇒ q :+ (q.max + 1)).iterate(2)(_.tail))
  .build(Diagram.toStringCaption(_).withAnchor("queue"))
  .render("queue"))

Vectors

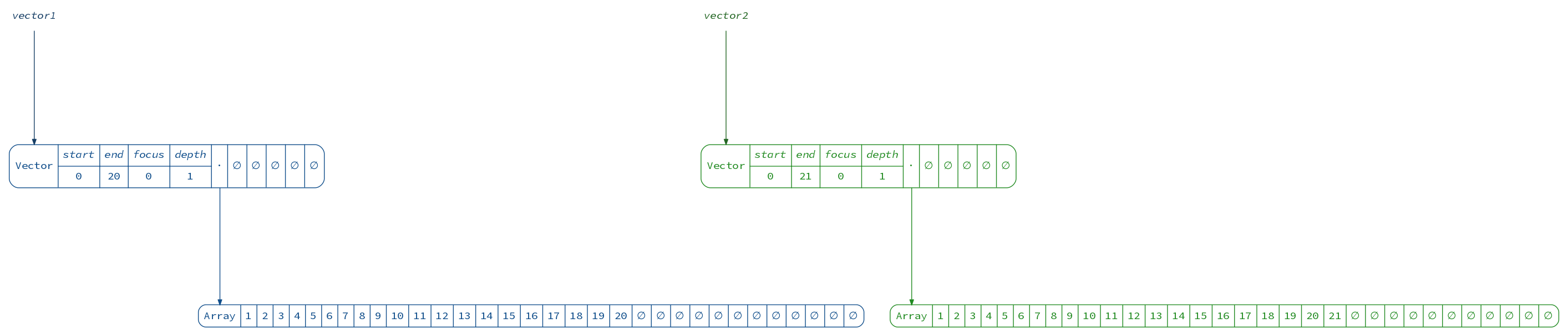
One downside common to both lists and queues we saw before is that to get an element by index, we need to potentially traverse the whole structure. A Vector is a powerful data structure addressing this shortcoming and available in Scala (among other languages, like Clojure).

Internally vectors utilize up to 6 layers of arrays, where 32 elements sit on the first layer, 1024 — on the second, 32^3 — on the third, etc. Therefore getting any element by its index requires at most 6 pointer dereferences, which can be deemed constant time (yes, the trick is that the number of elements that can be stored is limited by 2^31).

The internal 32-element arrays form the basic structural sharing blocks. For small vectors they will be recreated on most operations:

scala> val vector1 = (1 to 20).toVector
vector1: Vector[Int] = Vector(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20)

scala> val vector2 = vector1 :+ 21
vector2: scala.collection.immutable.Vector[Int] = Vector(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21)

(diagram(vector1) + diagram(vector2)).render("vectors", _.withVerticalSpacing(2))

However as more layers leap into action, a huge chunk of the data can be shared:

scala> val vector1 = (1 to 100).toVector
vector1: Vector[Int] = Vector(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100)

scala> val vector2 = vector1 :+ 21
vector2: scala.collection.immutable.Vector[Int] = Vector(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 21)

(diagram(vector1) + diagram(vector2)).render("big-vectors", _.withVerticalSpacing(2))

If you want to know more, this structure is covered in great detail by Jean Niklas L’orange in his blog. I also highly recommend watching this talk by Daniel Spiewak.

Finger Trees

To conclude this section, I would like to share a slightly less popular, but beautifully designed data structure called “finger tree” described in this paper by Hinze and Paterson. Enjoy the read and this animation of a finger tree getting filled with some numbers:

import de.sciss.fingertree.{FingerTree, Measure}
import reftree.contrib.FingerTreeInstances._

implicit val measure = Measure.Indexed

Animation
  .startWith(FingerTree(1))
  .iterateWithIndex(21)((t, i) ⇒ t :+ (i + 1))
  .build(Diagram(_).withCaption("Finger Tree").withAnchor("tree"))
  .render("finger", _.withDensity(75).withVerticalSpacing(2))

Lenses

So far we were looking into “standard” data structures, but in our code we often have to deal with custom data structures comprising our domain model. Updating this sort of data can be tricky if it’s immutable. For case classes Scala gives us the copy method:

case class Employee(
  name: String,
  salary: Long
)

scala> employee
res8: reftree.demo.Data.Employee = Employee(Michael,4000)

scala> val raisedEmployee = employee.copy(salary = employee.salary + 10)
raisedEmployee: reftree.demo.Data.Employee = Employee(Michael,4010)

However once composition comes into play, the resulting nested immutable data structures would require a lot of copy calls:

case class Employee(
  name: String,
  salary: Long
)

case class Startup(
  name: String,
  founder: Employee,
  team: List[Employee]
)

scala> startup
res9: reftree.demo.Data.Startup = Startup(Acme,Employee(Michael,4000),List(Employee(Adam,2100), Employee(Bella,2100), Employee(Chad,1980), Employee(Delia,1850)))

scala> val raisedFounder = startup.copy(
     |   founder = startup.founder.copy(
     |     salary = startup.founder.salary + 10
     |   )
     | )
raisedFounder: reftree.demo.Data.Startup = Startup(Acme,Employee(Michael,4010),List(Employee(Adam,2100), Employee(Bella,2100), Employee(Chad,1980), Employee(Delia,1850)))

// extra declarations for this section
import reftree.contrib.SimplifiedInstances.list
import reftree.contrib.OpticInstances._

val renderer = Renderer(
  renderingOptions = RenderingOptions(density = 75),
  directory = Paths.get(ImagePath, "immutability", "lenses")
)
import renderer._

(diagram(startup) + diagram(raisedFounder)).render("startup")

Ouch!

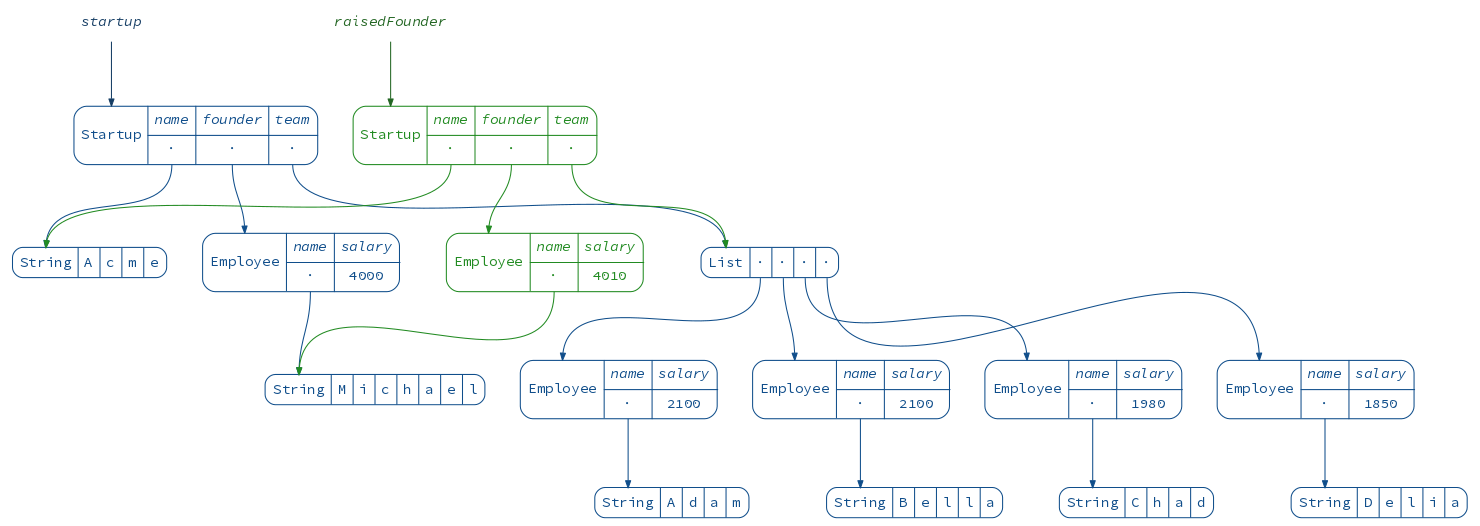
A common solution to this problem is a “lens”. In the simplest case a lens is a pair of functions to get and set a value of type B inside a value of type A. It’s called a lens because it focuses on some part of the data and allows to update it. For example, here is a lens that focuses on an employee’s salary (using the excellent Monocle library):

scala> import monocle.macros.GenLens
import monocle.macros.GenLens

scala> val salaryLens = GenLens[Employee](_.salary)
salaryLens: monocle.Lens[reftree.demo.Data.Employee,Long] = $anon$1@4bfef05a

scala> salaryLens.get(startup.founder)
res13: Long = 4000

scala> salaryLens.modify(s => s + 10)(startup.founder)
res14: reftree.demo.Data.Employee = Employee(Michael,4010)

diagram(OpticFocus(salaryLens, startup.founder)).render("salaryLens")

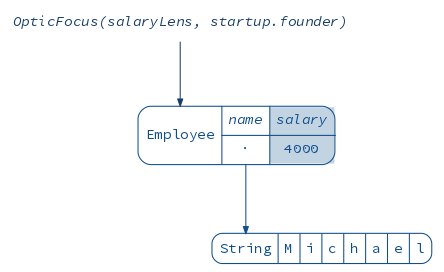
We can also define a lens that focuses on the startup’s founder:

scala> val founderLens = GenLens[Startup](_.founder)
founderLens: monocle.Lens[reftree.demo.Data.Startup,reftree.demo.Data.Employee] = $anon$1@44f414f0

scala> founderLens.get(startup)
res16: reftree.demo.Data.Employee = Employee(Michael,4000)

diagram(OpticFocus(founderLens, startup)).render("founderLens")

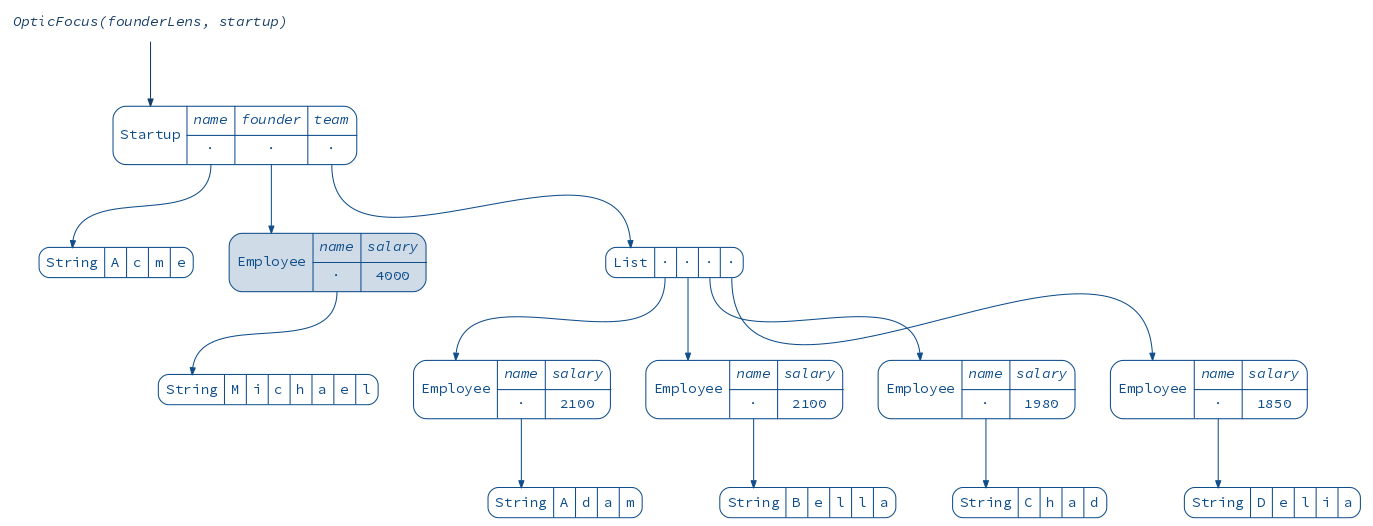
It’s not apparent yet how this would help, but the trick is that lenses can be composed:

scala> val founderSalaryLens = founderLens composeLens salaryLens
founderSalaryLens: monocle.PLens[reftree.demo.Data.Startup,reftree.demo.Data.Startup,Long,Long] = monocle.PLens$$anon$1@46b9b8ee

scala> founderSalaryLens.get(startup)
res18: Long = 4000

scala> founderSalaryLens.modify(s => s + 10)(startup)
res19: reftree.demo.Data.Startup = Startup(Acme,Employee(Michael,4010),List(Employee(Adam,2100), Employee(Bella,2100), Employee(Chad,1980), Employee(Delia,1850)))

diagram(OpticFocus(founderSalaryLens, startup)).render("founderSalaryLens")

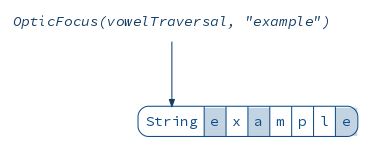
One interesting thing is that lenses can focus on anything, not just direct attributes of the data. Here is a traversal — a more generic kind of lens — that focuses on all vowels in a string:

diagram(OpticFocus(vowelTraversal, "example")).render("vowelTraversal")

We can use it to give our founder a funny name:

scala> val employeeNameLens = GenLens[Employee](_.name)
employeeNameLens: monocle.Lens[reftree.demo.Data.Employee,String] = $anon$1@673ec069

scala> val founderVowelTraversal = founderLens composeLens employeeNameLens composeTraversal vowelTraversal
founderVowelTraversal: monocle.PTraversal[reftree.demo.Data.Startup,reftree.demo.Data.Startup,Char,Char] = monocle.PTraversal$$anon$2@2784a907

scala> founderVowelTraversal.modify(v => v.toUpper)(startup)
res22: reftree.demo.Data.Startup = Startup(Acme,Employee(MIchAEl,4000),List(Employee(Adam,2100), Employee(Bella,2100), Employee(Chad,1980), Employee(Delia,1850)))

diagram(OpticFocus(founderVowelTraversal, startup)).render("founderVowelTraversal")

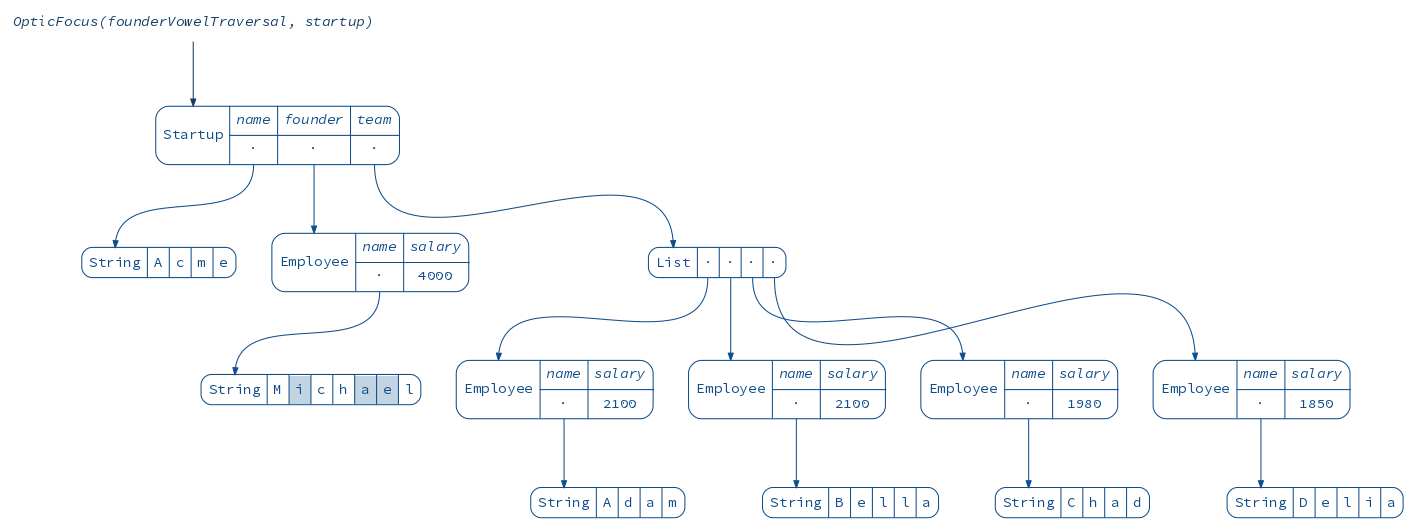
So far we have replaced the copy boilerplate with a number of lens declarations. However most of the time our goal is just to update data.

In Scala there is a great library called quicklens that allows to do exactly that, creating all the necessary lenses under the hood:

scala> import com.softwaremill.quicklens._
import com.softwaremill.quicklens._

scala> val raisedCeo = startup.modify(_.founder.salary).using(s => s + 10)
raisedCeo: reftree.demo.Data.Startup = Startup(Acme,Employee(Michael,4010),List(Employee(Adam,2100), Employee(Bella,2100), Employee(Chad,1980), Employee(Delia,1850)))

You might think this is approaching the syntax for updating mutable data, but actually we have already surpassed it, since lenses are much more flexible:

scala> val raisedEveryone = startup.modifyAll(_.founder.salary, _.team.each.salary).using(s => s + 10)
raisedEveryone: reftree.demo.Data.Startup = Startup(Acme,Employee(Michael,4010),List(Employee(Adam,2110), Employee(Bella,2110), Employee(Chad,1990), Employee(Delia,1860)))

Zippers

In our domain models we are often faced with recursive data structures. Consider this example:

case class Employee(
  name: String,
  salary: Long
)

case class Hierarchy(
  employee: Employee,
  team: List[Hierarchy]
)

case class Company(
  name: String,
  hierarchy: Hierarchy
)

The Hierarchy class refers to itself. Let’s grab a company object and display its hierarchy as a tree:

// extra declarations for this section
import zipper._
import reftree.contrib.SimplifiedInstances.option
import reftree.contrib.ZipperInstances._

val renderer = Renderer(
  renderingOptions = RenderingOptions(density = 100),
  directory = Paths.get(ImagePath, "immutability", "zippers")
)
import renderer._

diagram(company.hierarchy).render("company")

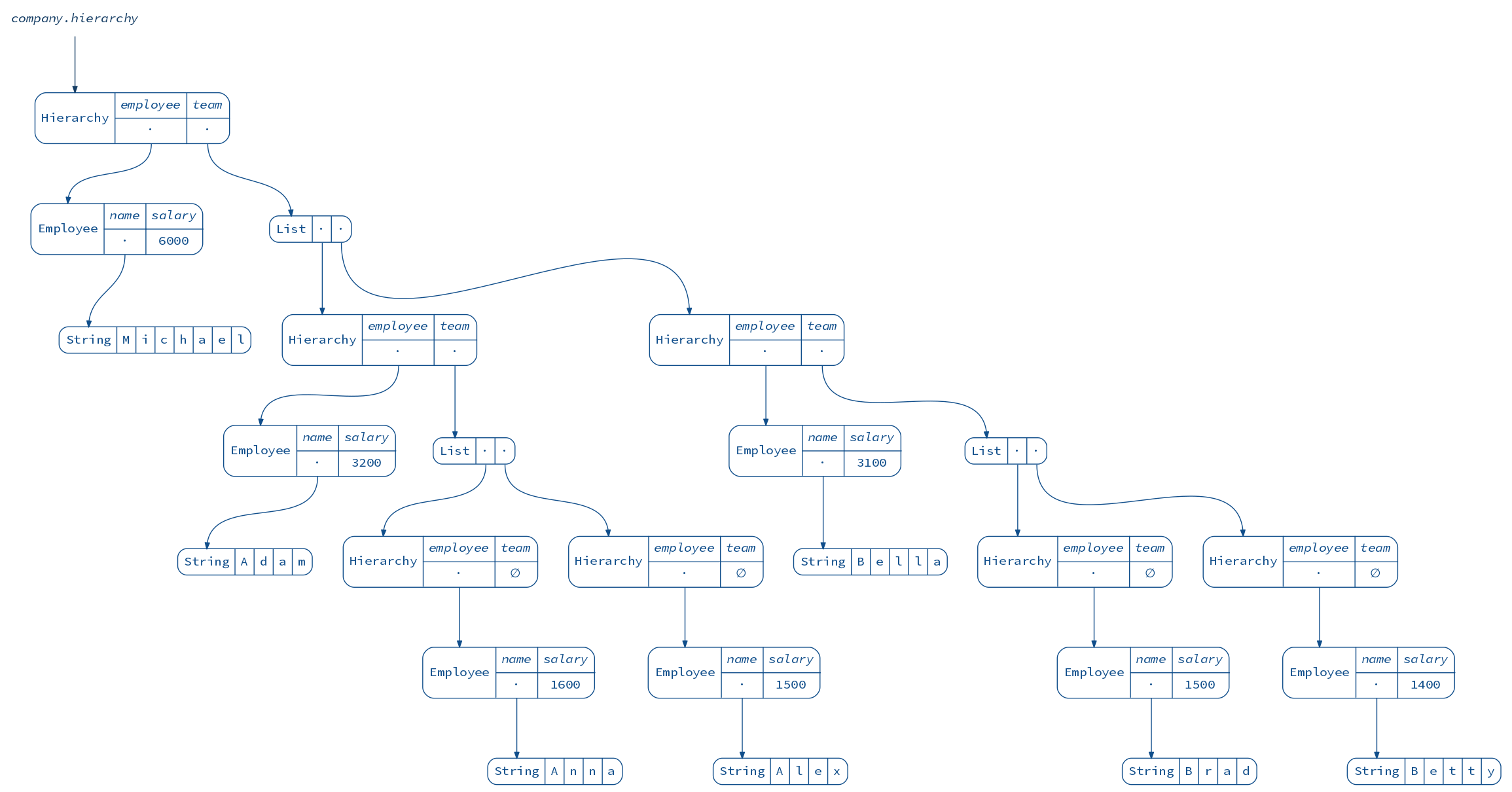
What if we want to navigate through this tree and modify it along the way? We can use lenses, but the recursive nature of the tree allows for a better solution.

This solution is called a “Zipper”, and was introduced by Gérard Huet in 1997. It consists of a “cursor” pointing to a location anywhere in the tree — “current focus”. The cursor can be moved freely with operations like moveDownLeft, moveRight, moveUp, etc. Current focus can be updated, deleted, or new nodes can be inserted to its left or right. Zippers are immutable, and every operation returns a new Zipper. All the changes made to the tree can be committed, yielding a new modified version of the original tree.

Here is how we would insert a new employee into the hierarchy:

val updatedHierarchy = Zipper(company.hierarchy).moveDownRight.moveDownRight.insertRight(newHire).commit

(diagram(company.hierarchy) + diagram(updatedHierarchy)).render("updatedHierarchy")

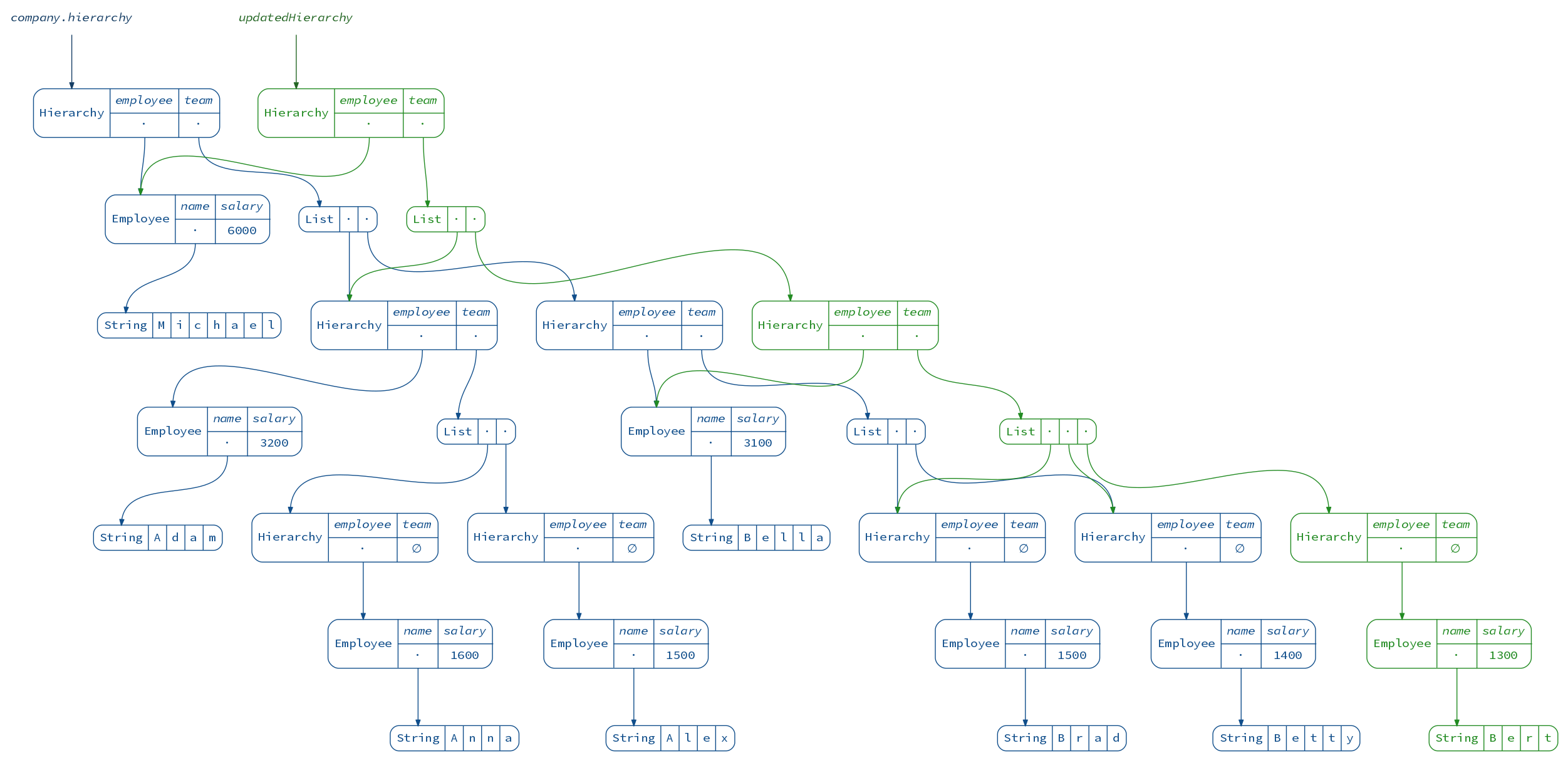
My zipper library provides a few useful movements and operations.

Let’s consider a simpler recursive data structure:

case class Tree(x: Int, c: List[Tree] = List.empty)

and a simple tree:

scala> simpleTree
res28: reftree.demo.Data.Tree = Tree(1,List(Tree(2,List()), Tree(3,List()), Tree(4,List()), Tree(5,List(Tree(6,List()), Tree(7,List())))))

diagram(simpleTree).render("simpleTree")

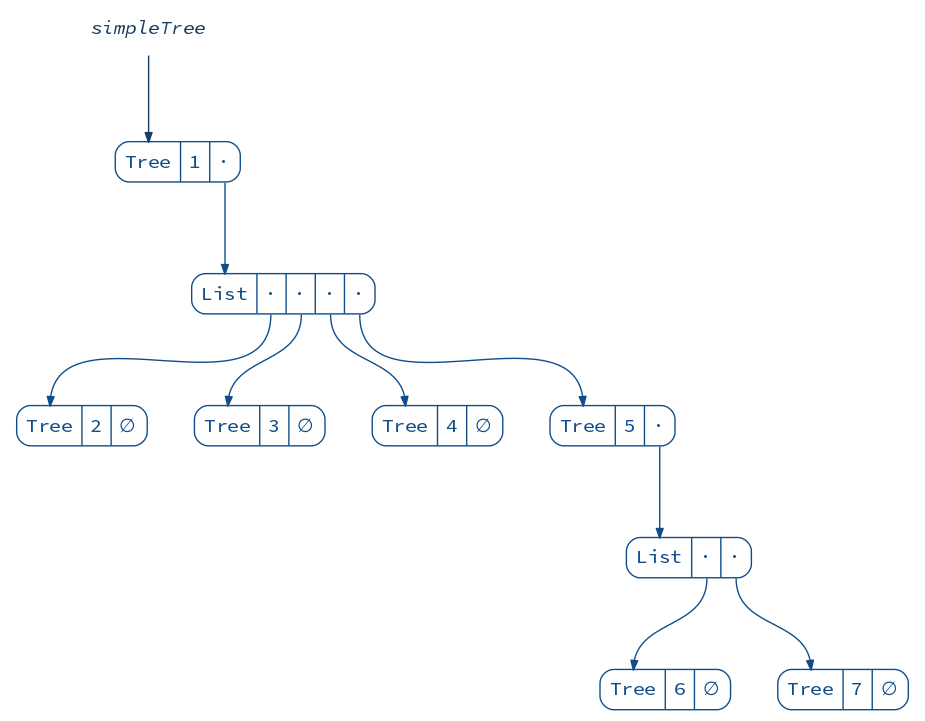
When we wrap a Zipper around this tree, it does not look very interesting yet:

val zipper1 = Zipper(simpleTree)

(diagram(simpleTree) + diagram(zipper1)).render("zipper1")

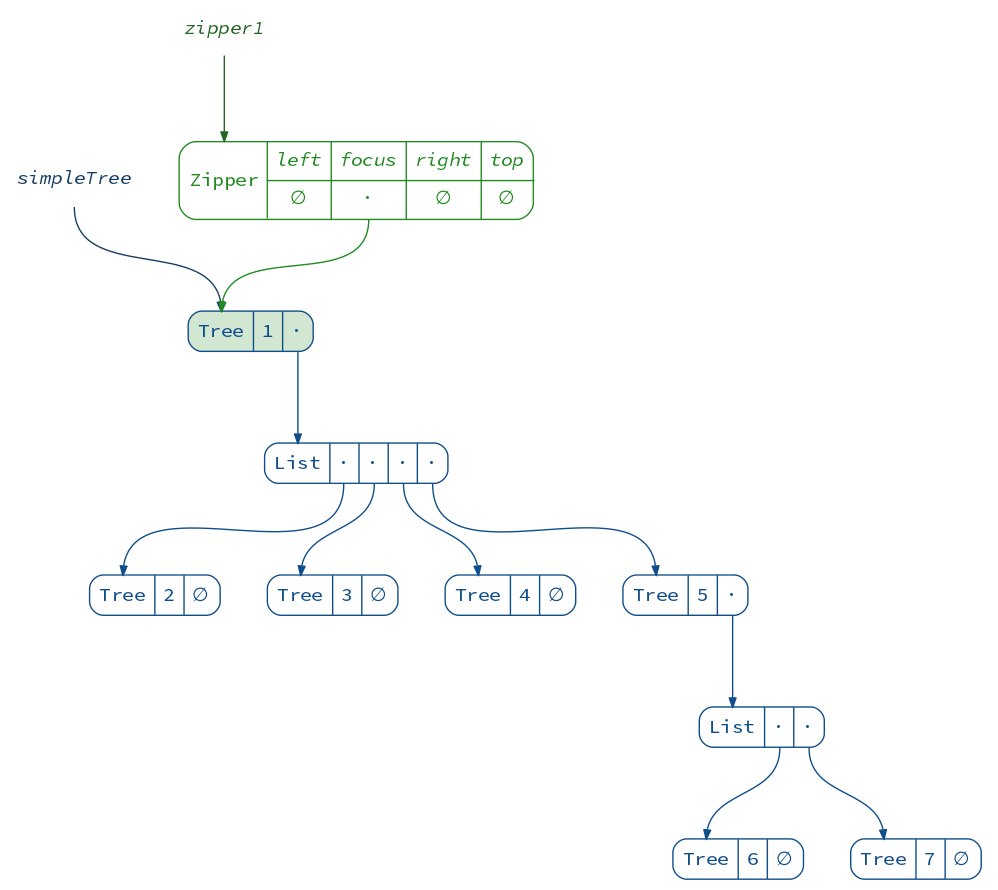
We can see that it just points to the original tree and has some other empty fields. More specifically, a Zipper consists of four pointers:

case class Zipper[A](
  left: List[A],           // left siblings of the focus
  focus: A,                // the current focus
  right: List[A],          // right siblings of the focus
  top: Option[Zipper[A]]   // the parent zipper
)

In this case the focus is the root of the tree, which has no siblings, and the parent zipper does not exist, since we are at the top level.

One thing we can do right away is modify the focus:

val zipper2 = zipper1.update(focus ⇒ focus.copy(x = focus.x + 99))

(diagram(simpleTree) + diagram(zipper1) + diagram(zipper2)).render("zipper2")

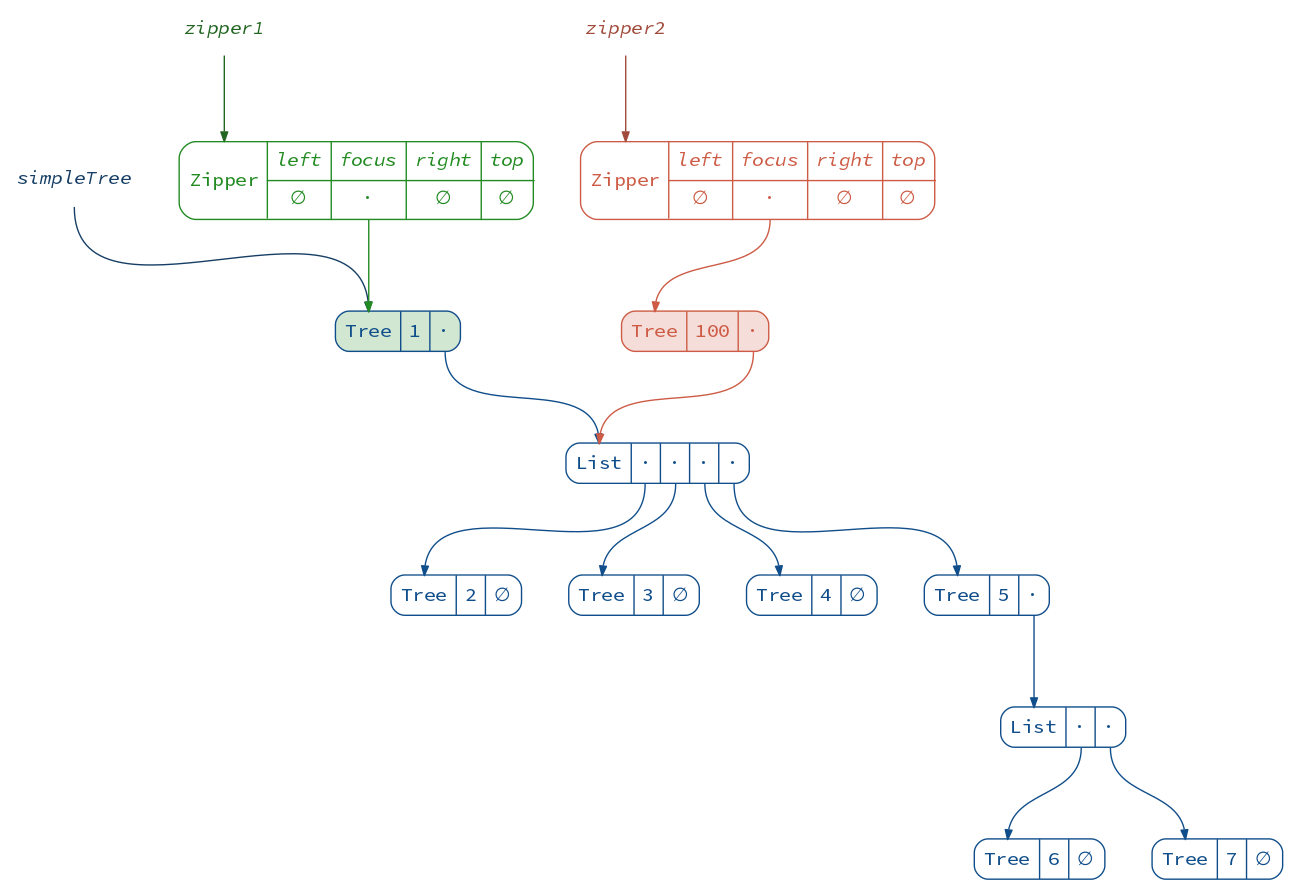
We just created a new tree! To obtain it, we have to commit the changes:

val tree2 = zipper2.commit

(diagram(simpleTree) + diagram(tree2)).render("tree2")

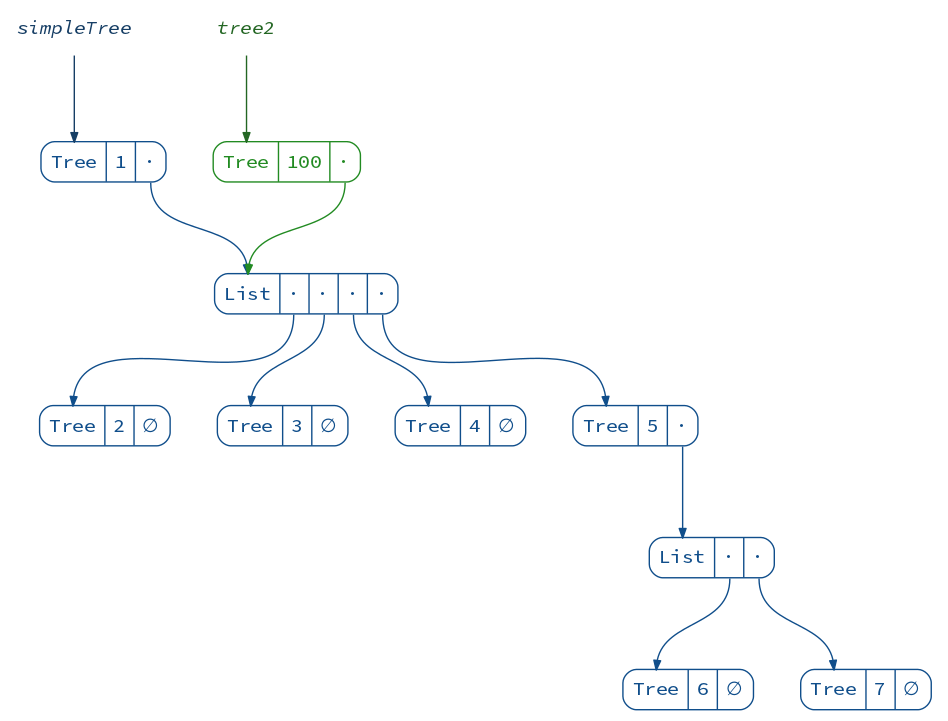
If you were following closely, you would notice that nothing spectacular happened yet: we could’ve easily obtained the same result by modifying the tree directly:

val tree2b = simpleTree.copy(x = simpleTree.x + 99)

assert(tree2b == tree2)

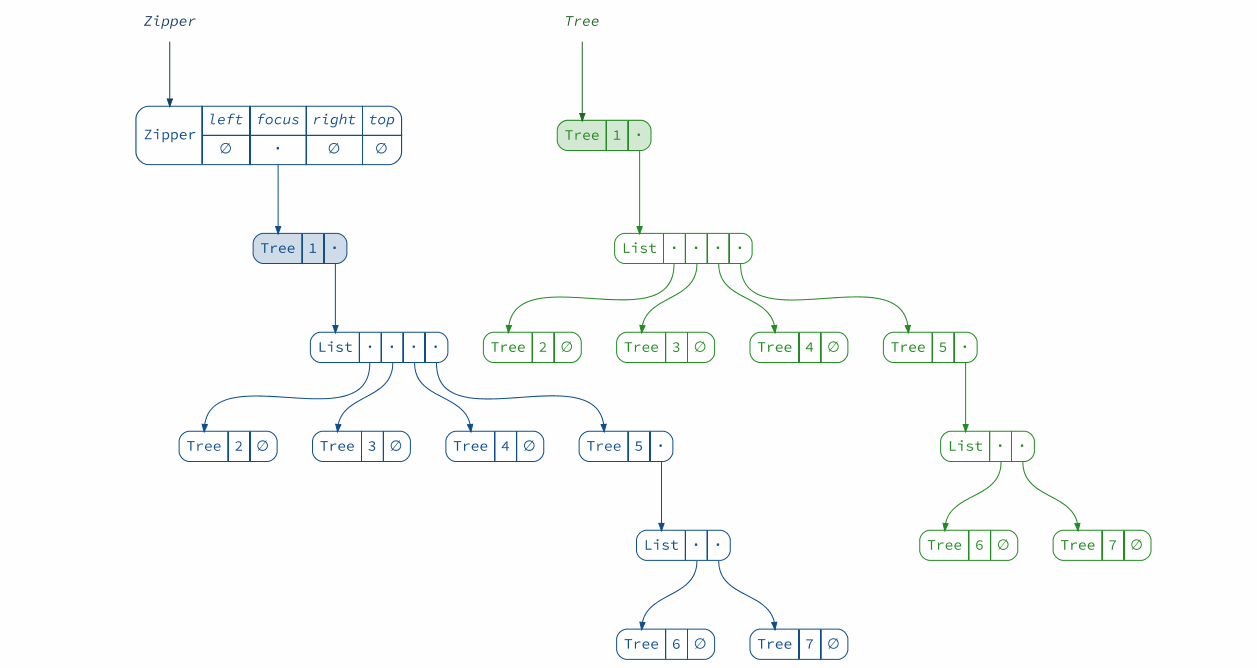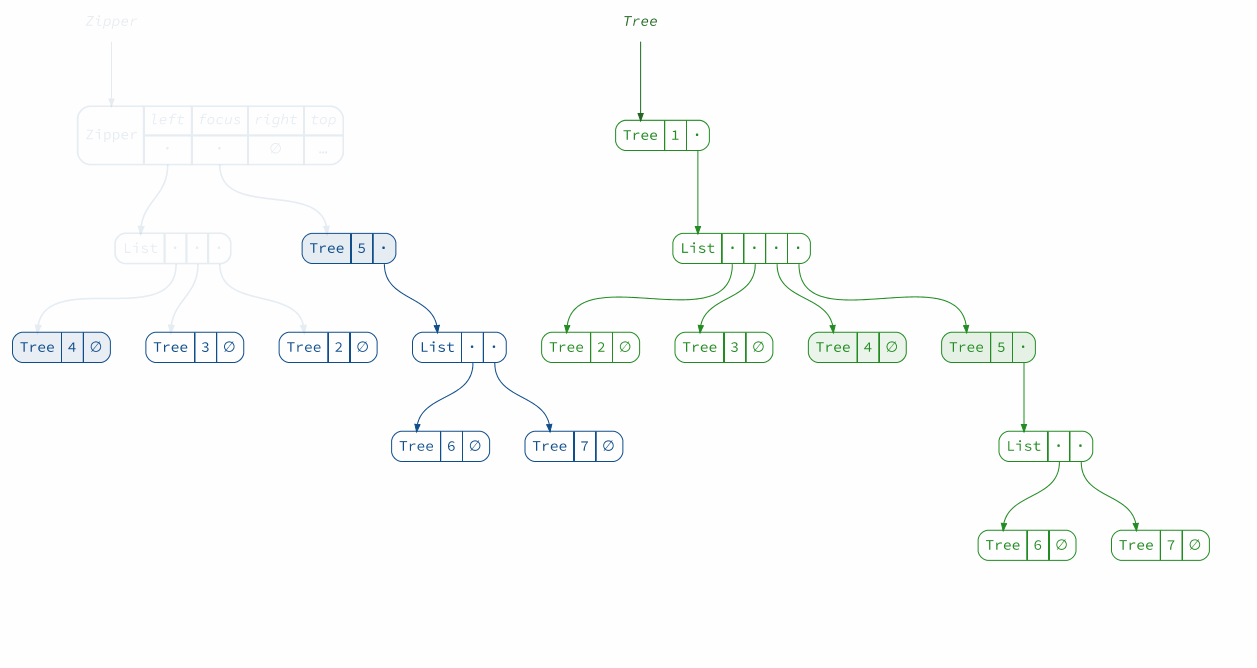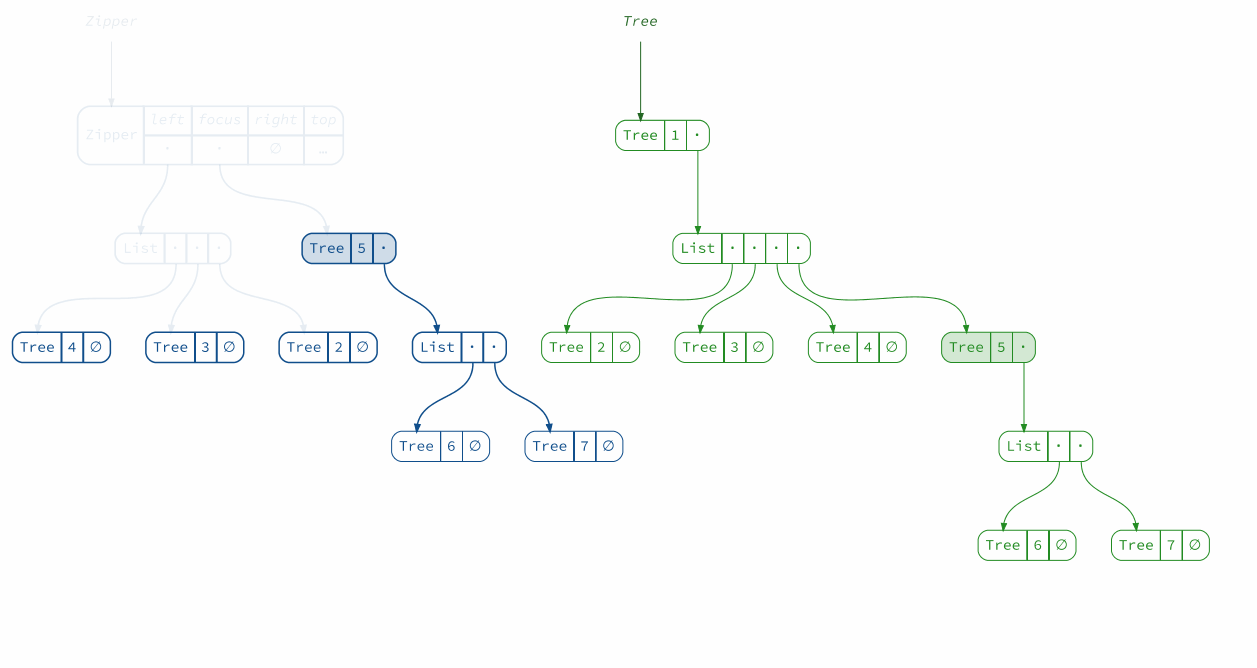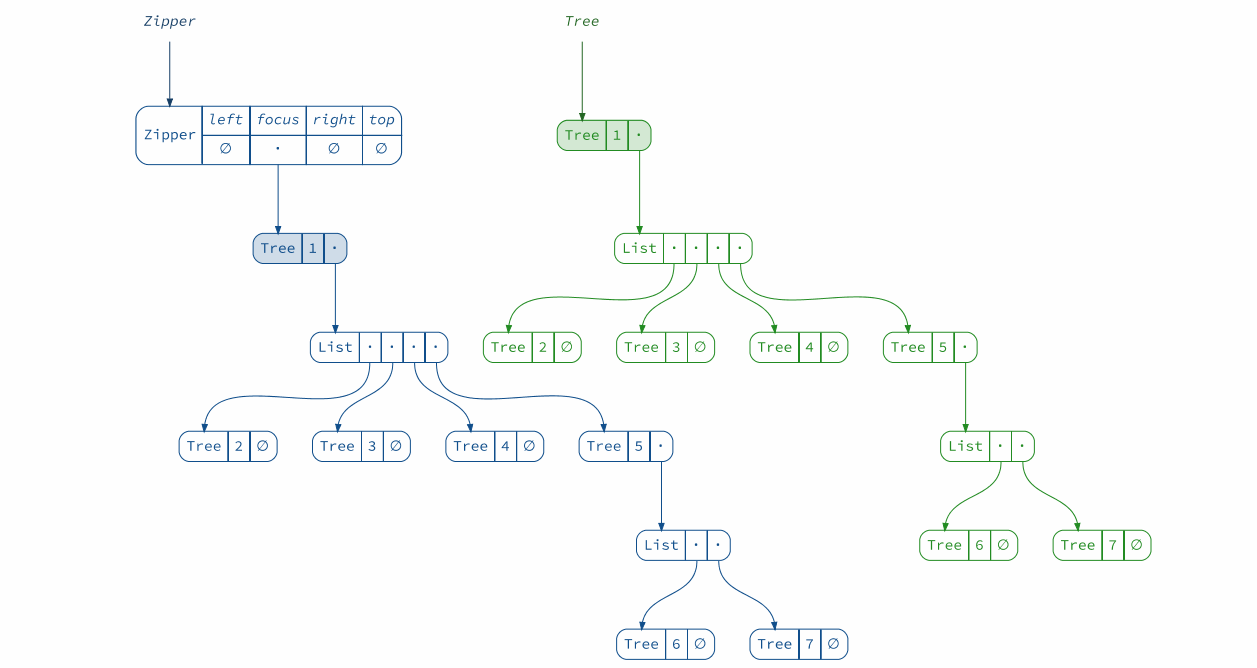
The power of Zipper becomes apparent when we go one or more levels deep. To move down the tree, we “unzip” it, separating the child nodes into the focused node and its left and right siblings:

val zipper2 = zipper1.moveDownLeft

(diagram(zipper1) + diagram(zipper2)).render("zipper1+2")

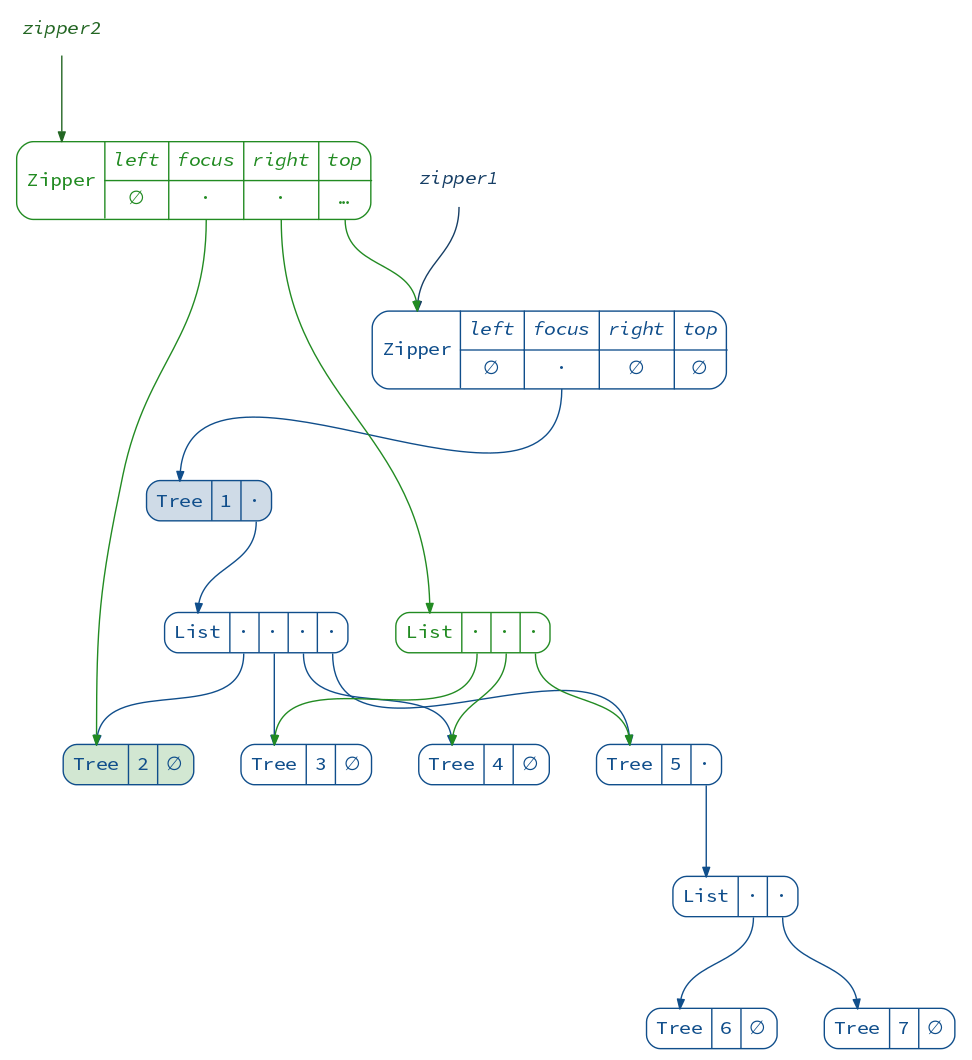
The new Zipper links to the old one, which will allow us to return to the root of the tree when we are done applying changes. This link however prevents us from seeing the picture clearly. Let’s look at the second zipper alone:

diagram(zipper2).render("zipper2b")

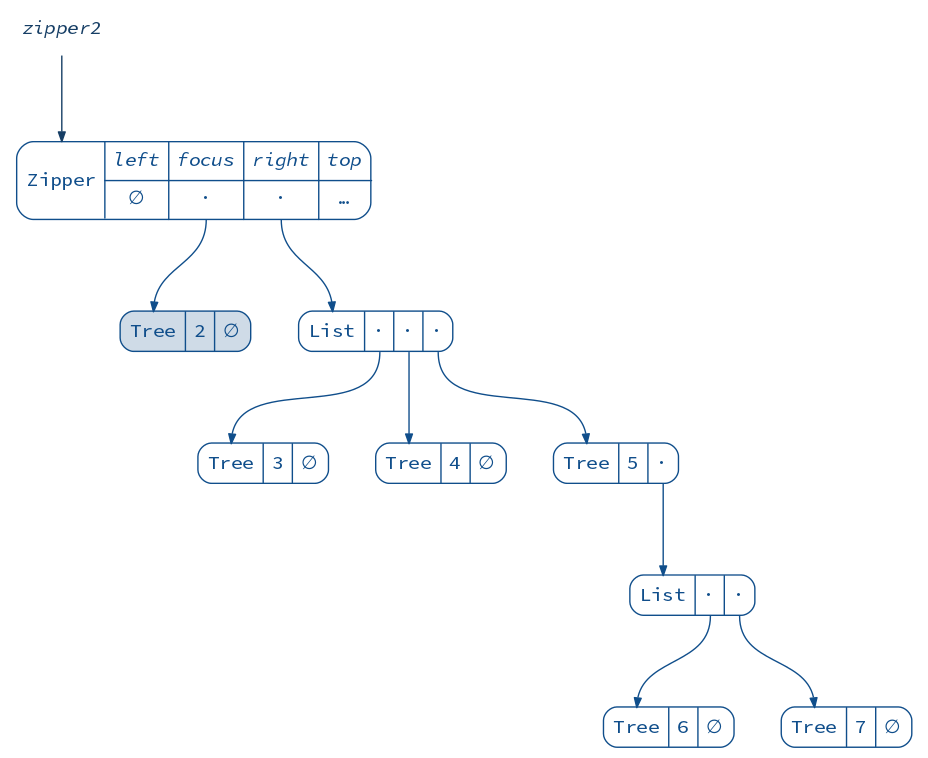
Great! We have 2 in focus and 3, 4, 5 as right siblings. What happens if we move right a bit?

val zipper3 = zipper2.moveRightBy(2)

diagram(zipper3).render("zipper3")

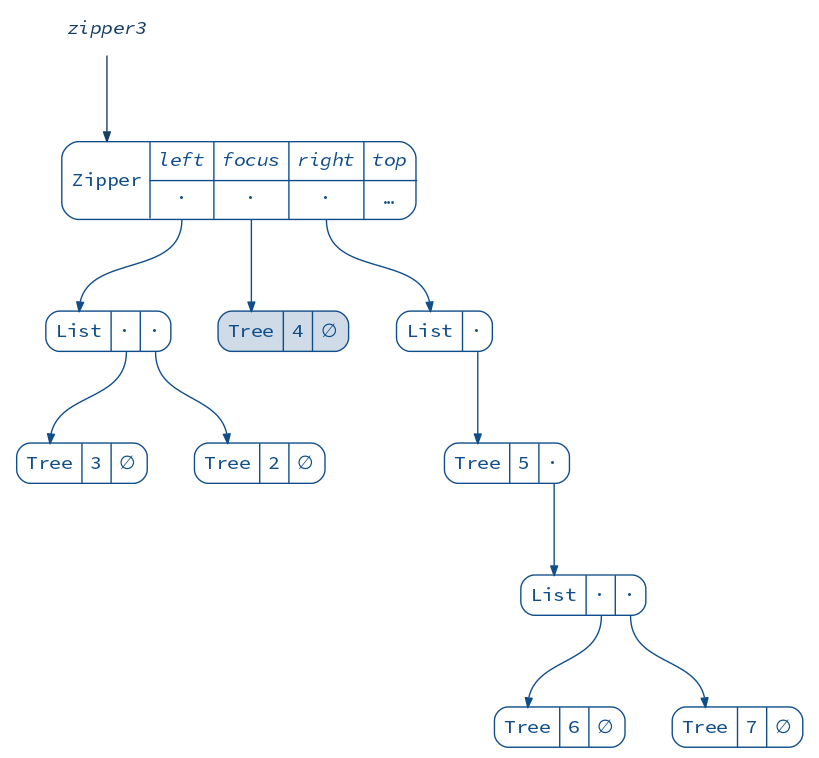
This is interesting! Notice that the left siblings are “inverted”. This allows to move left and right in constant time, because the sibling adjacent to the focus is always at the head of the list.

This also allows us to insert new siblings easily:

val zipper4 = zipper3.insertLeft(Tree(34))

diagram(zipper4).render("zipper4")

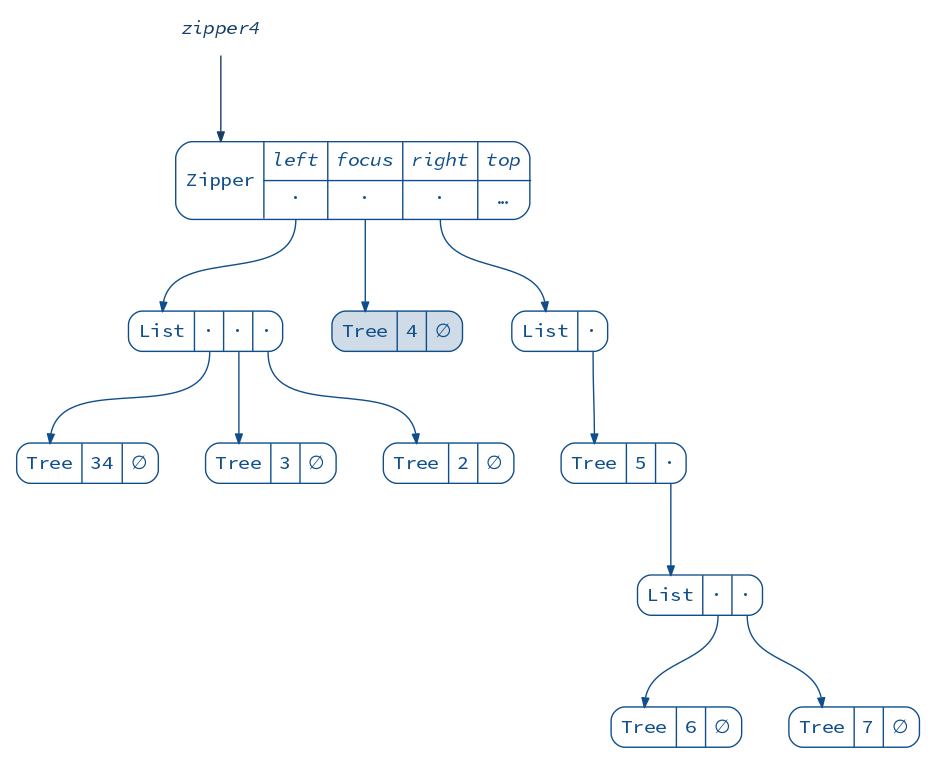
And, as you might know, we can delete nodes and update the focus:

val zipper5 = zipper4.deleteAndMoveRight.set(Tree(45))

diagram(zipper5).render("zipper5")

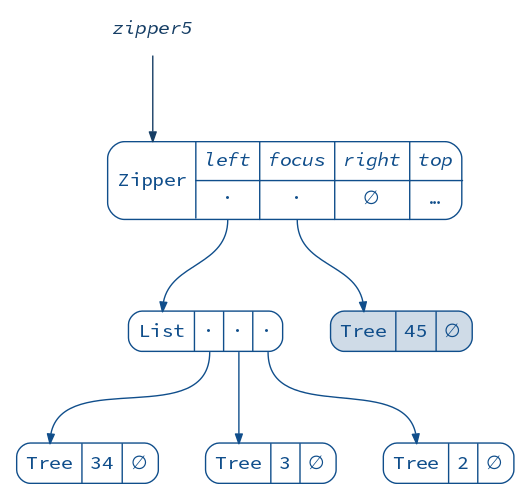
Finally, when we move up, the siblings at the current level are “zipped” together and their parent node is updated:

val zipper6 = zipper5.moveUp

diagram(zipper6).render("zipper6")

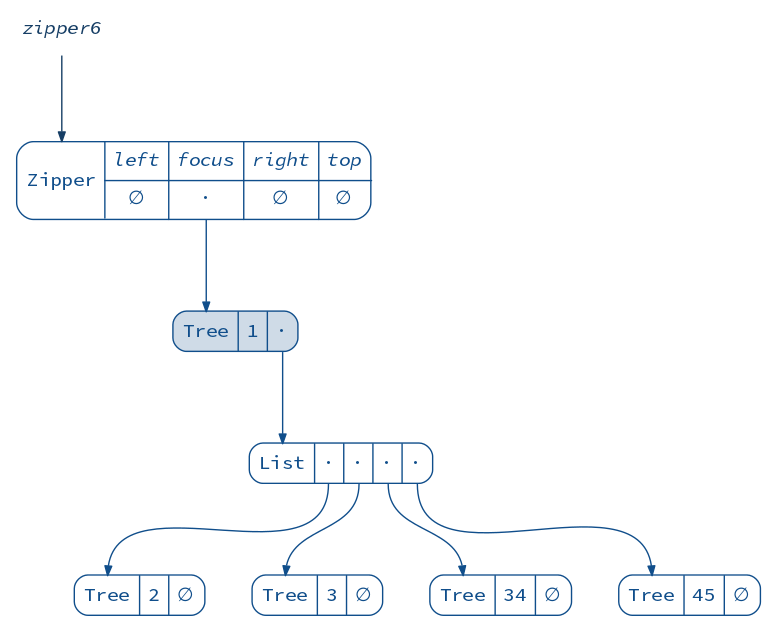
You can probably guess by now that .commit is a shorthand for going all the way up (applying all the changes) and returning the focus:

val tree3a = zipper5.moveUp.focus
val tree3b = zipper5.commit

assert(tree3a == tree3b)

Here is an animation of the navigation process:

val movement = Animation
  .startWith(Zipper(Data.simpleTree))
  .iterate(
    _.moveDownLeft,
    _.moveRight, _.moveRight, _.moveRight,
    _.moveDownLeft,
    _.moveRight, _.moveLeft,
    _.top.get,
    _.moveLeft, _.moveLeft, _.moveLeft,
    _.top.get
  )

val trees = movement
  .build(z ⇒ Diagram(ZipperFocus(z, Data.simpleTree)).withCaption("Tree").withAnchor("tree"))
  .toNamespace("tree")

val zippers = movement
  .build(Diagram(_).withCaption("Zipper").withAnchor("zipper").withColor(2))
  .toNamespace("zipper")

(trees + zippers).render("tree+zipper")

Useful resources

Books, papers and talks

Purely functional data structures by Chris Okasaki, and/or his PhD thesis — the introduction to immutable data structures
What’s new in purely functional data structures since Okasaki — an excellent StackExchange answer with pointers for further reading
Extreme cleverness by Daniel Spiewak — a superb talk covering several immutable data structures (implemented here)
Understanding Clojure’s Persistent Vectors, part 1 and part 2 — a series of blog posts by Jean Niklas L’orange
Finger Trees and 1-2 Brother Trees described by Hinze and Paterson
Huet’s original Zipper paper — a great short read introducing the Zipper
Weaving a web by Hinze and Jeuring — another interesting Zipper-like approach

Scala libraries

zipper — my Zipper implementation
Monocle — an “optics” library
Quicklens — a simpler way to update nested case classes
FingerTree — an implementation of the Finger Tree data structure

Unzipping immutability